平均値から正規分布乱数を生成する方法（PHP）

テスト用データを作成する時に正規分布（ガウス分布）に沿ったデータを利用すると、よりリアルなデータテストが行えます。
しかし、話を極端にしてデータが平均値しかなかった場合はどうやって正規分布乱数を作成したら良いのでしょう？

Normal関数を作って利用

Pythonではライブラリ（Numpy）で簡単にnormal()を使って標準正規分布に沿った乱数生成ができますが、PHPでは標準でnormal()関数がありません。
そこでネットでウロウロしたところ、ボックスミュラー法を利用したPHP版のnormal()があったので、下記に掲載します。

normal()関数

<?php
/**
 * 正規分布に沿った乱数を生成する
 *
 * @param float $av 平均値
 * @param float $sd 標準偏差
 * @return float
 */
function normal($av, $sd){
    $x=mt_rand()/mt_getrandmax();
    $y=mt_rand()/mt_getrandmax();
    return sqrt(-2*log($x))*cos(2*pi()*$y)*$sd+$av;
}
?>

引数の１つめは平均値、２つめは標準偏差です。

標準偏差に何を指定すればいいの？

標準偏差は、分かりやすく言うと「『平均値からデータそれぞれがどれくらい散らばっているか』の平均値」ですが、そういった値が得られない場合は、±2σや±3σの理論を利用しましょう。
例えば平均値から±3σの範囲にある乱数を生成したいのであれば「平均値 ÷ 3.0 ≒ 標準偏差」として標準偏差を求めます。

要するにここで求めたいのはデータの限界値（上限、下限）なので「限界値 = 平均値 + (平均値 ÷ 3 × 3) = 平均値の2倍（または2分の1）」にするという理論です。

仮に平均値が500とすると、標準偏差は 500÷ 3.0 = 166.66666… になります。
実際に+3σの位置にある値を算出すると 3 × 166.66666… + 500 = 1000.00000…1 ≒ 1000 になります。
逆に-3σを計算すると0.00000…1 ≒ 0 になります。
これは0～1,000の間（中心が500）で正規分布の乱数を生成する場合に都合が良い値として利用できます。

実際に作成してみる

以下にnormal()を使ったサンプルPHPプログラムを掲載します。

<?php
/**
 * サンプル
 * 平均値500で最大幅±3.0σの正規乱数を1000個生成する
 */
$av = 500;
$sg = 3.0;
$lp = 1000;
$sd = $av / $sg;
for ($i=0;$i<$lp;$i++) {
    echo normal($av, $sd) . "\n";
}
?>

生成された乱数をExcelにコピペして正規表現グラフを作成してみます。
参考：正規分布(ガウス分布)のグラフを作成

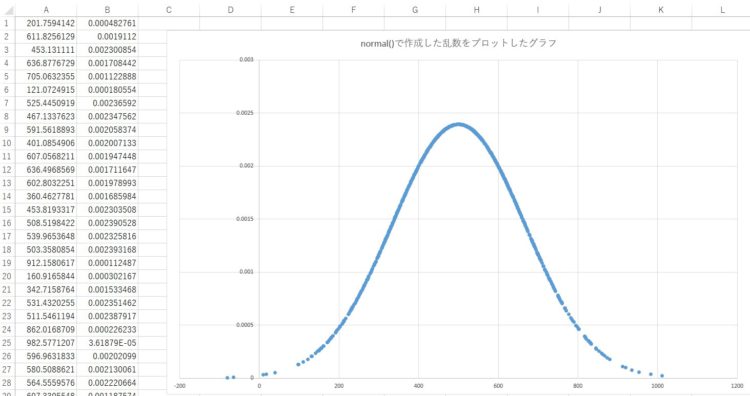
ダウンロード：正規乱数グラフ.xlsx
このように、いくつかの外れ値があるものの、自然な正規分布に沿った0～1000までの乱数が生成できていることがわかります。